ワグスタッフ素数

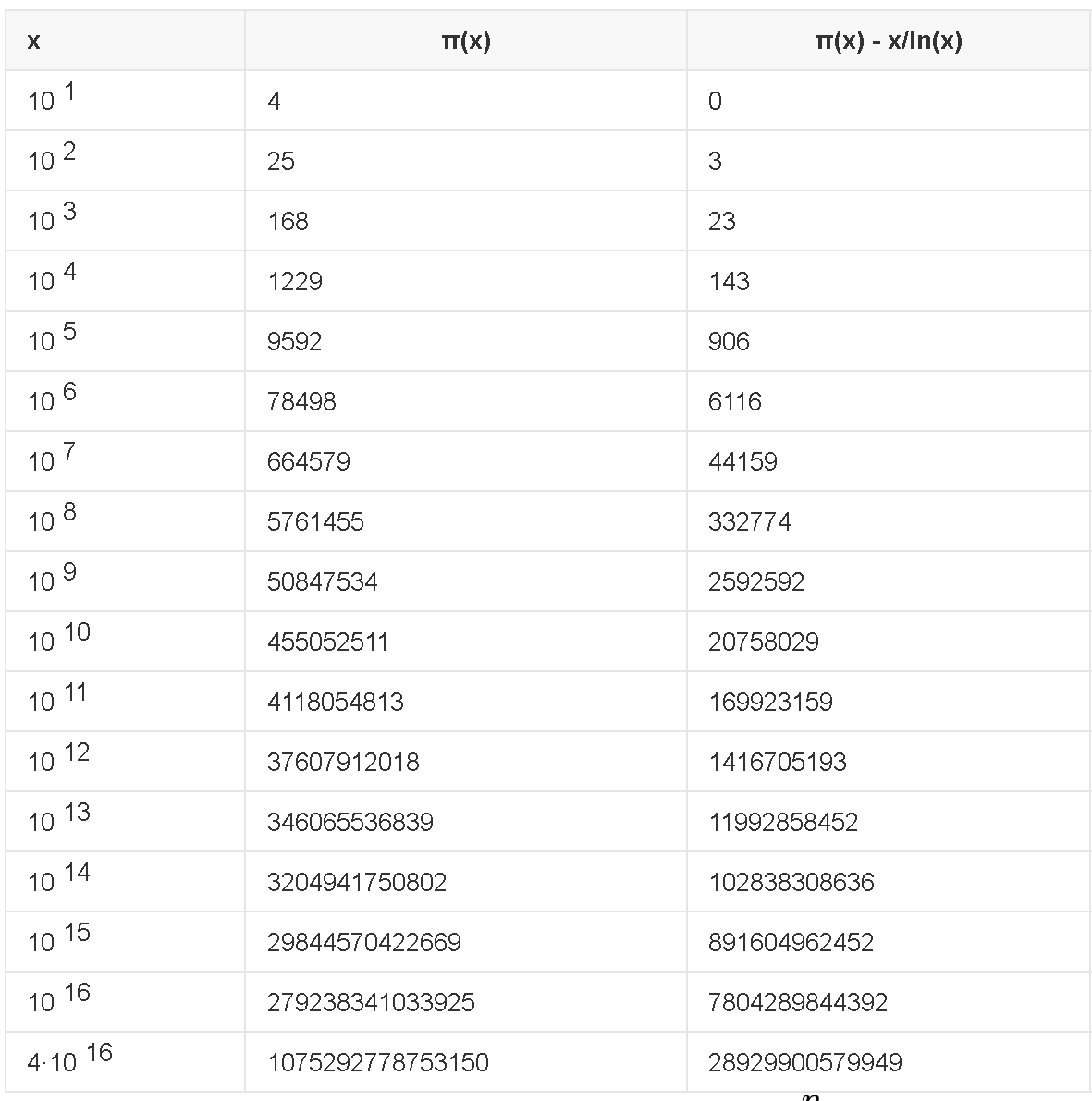
数論において、ワグスタッフ素数（英: Wagstaff prime）は、

${\displaystyle p={{2^{q} 1} \over 3}}$

の形をした素数 p である。ただし q は別の素数である。ワグスタッフ素数は、数学者のサミュエル S. ワグスタッフ・ジュニアにあやかって名付けられた。Prime Pages では、フランソワ・モランが Eurocrypt の 1990年 の学会での講演において、この素数を名付けた事に言及している。ワグスタッフ素数は新メルセンヌ予想と関連しており、暗号理論への応用を持っている。

主な素数

最初の3つのワグスタッフ素数は、3, 11, 43 である。なぜならば

${\displaystyle {\begin{aligned}3&={2^{3} 1 \over 3},\\[5pt]11&={2^{5} 1 \over 3},\\[5pt]43&={2^{7} 1 \over 3}.\end{aligned}}}$

知られているワグスタッフ素数

最初のいくつかのワグスタッフ素数は以下のものである。

3, 11, 43, 683, 2731, 43691, 174763, 2796203, 715827883, 2932031007403, … オンライン整数列大辞典の数列 A000979

2013年10月の時点で、ワグスタッフ素数か確率的素数（PRP)になるとわかっている指数${\displaystyle q}$を、小さい順に並べると以下のようになる。

3, 5, 7, 11, 13, 17, 19, 23, 31, 43, 61, 79, 101, 127, 167, 191, 199, 313, 347, 701, 1709, 2617, 3539, 5807, 10501, 10691, 11279, 12391, 14479, 42737, 83339, 95369, 117239, 127031, 138937, 141079, 267017, 269987, 374321, 986191, 4031399, …, 13347311, 13372531 オンライン整数列大辞典の数列 A000978

2010年2月に、Tony Reix が次のワグスタッフ確率的素数を発見した。

${\displaystyle {\frac {2^{4031399} 1}{3}}}$

これは 1,213,572 桁の数であり、当時見つかっていた中で3番目に大きい確率的素数であった。

2013年9月、Ryan Propper はさらに2つのワグスタッフ確率的素数の発見を知らせた。

${\displaystyle {\frac {2^{13347311} 1}{3}}}$

と

${\displaystyle {\frac {2^{13372531} 1}{3}}}$

である。いずれも400万桁よりわずかに多い桁数をもった確率的素数である。4031399 と 13347311 の間にワグスタッフ確率的素数を生み出す指数があるのかどうか、今のところ知られていない。

素数判定

これらの数は q の値が 83339 までのときは素数であることが証明されている。2020年12月 (2020-12)現在 q > 83339 のときは確率的素数である。 q = 42737 のときに素数であることの証明は François Morain によって、 Opteron processor上で 743 GHz-days 間ワークステーションのいくつかのネットワーク上で動作している分散された ECPP を実行することによって、2007 年になされた。それはその発見から2009年3月まででは ECPP による素数の証明では3番目に大きい素数であった。

今のところ知られているアルゴリズムで、ワグスタッフ数が素数であることを最も早く証明できるものは、ECPP である。

Jean Penné による LLR (Lucas-Lehmer-Riesel) ツールは、 Vrba-Reix test の手段でワグスタッフ確率的素数を見つけるために使われる。それはワグスタッフ数を法とした ${\displaystyle x^{2}-2}$ のもとでの digraph の周期性に基づいた PRP テストである

一般化

より一般的な次の形の数を考えることが自然である

${\displaystyle Q(b,n)={\frac {b^{n} 1}{b 1}}}$

ただし底は ${\displaystyle b\geq 2}$ である。${\displaystyle n}$ が奇数のときには

${\displaystyle {\frac {b^{n} 1}{b 1}}={\frac {(-b)^{n}-1}{(-b)-1}}=R_{n}^{(-b)}}$

であるので、これらの一般化されたワグスタッフ数は、負の底 ${\displaystyle -b}$ をもったレピュニット数のケースと考えられることがある。

いくつかの特定の ${\displaystyle b}$ の値について、（非常に小さい ${\displaystyle n}$ に対して例外があるかもしれないがそれを除いて）すべての ${\displaystyle Q(b,n)}$ は、「代数的な」分解のために合成数である。具体的には、${\displaystyle b}$ が奇数の指数をもった完全冪の形（例えば 8, 27, 32, 64, 125, 128, 216, 243, etc. オンライン整数列大辞典の数列 A070265）であれば、${\displaystyle m}$ が奇数のとき ${\displaystyle x^{m} 1}$ が ${\displaystyle x 1}$ で割り切れるという事実によって、これらの特殊な場合には ${\displaystyle Q(a^{m},n)}$ は ${\displaystyle a^{n} 1}$ で割り切れる。別のケースは k を正の整数として ${\displaystyle b=4k^{4}}$ のときである（例えば 4, 64, 324, 1024, 2500, 5184, etc. オンライン整数列大辞典の数列 A141046）。このとき aurifeuillean factorization がある。

しかしながら、${\displaystyle b}$ が代数的な分解をもたないときは、${\displaystyle Q(b,n)}$ が素数になる ${\displaystyle n}$ が無数に存在するという予想を立てることができる。（${\displaystyle b}$ ≤ 300 に対しては、素数や PRP が知られていない 9 つの底 97, 103, 113, 175, 186, 187, 188, 220, and 284 が存在し、PRP は知られているが素数であることが証明されていないような 7 つの底 53, 124, 150, 182, 205, 222, and 296 が存在する。リストを見よ。すべての n が奇素数であることに注意せよ。）

オンライン整数列大辞典の数列 A084742

b = 53, 124, 150, 182, 205, 222, 296 に対しては確率的素数しか存在ない。

b = 97, 103, 113, 175, 186, 187, 188, 220, 284 に対しては素数も PRP も知られていない。

代数的な分解のために、b = 8, 27, 32, 64, 125, 243 に対しては素数が存在しない。（b = 1 の場合はすべて 1 だが 1 は素数でない）

すべての奇素数がリストにあることが期待される。

${\displaystyle b=10}$ に対して、素数は次のように現れる。9091, 909091, 909090909090909091, 909090909090909090909090909091, … オンライン整数列大辞典の数列 A097209。また、これらの n は次のようになる。5, 7, 19, 31, 53, 67, 293, 641, 2137, 3011, 268207, ... オンライン整数列大辞典の数列 A001562。

${\displaystyle Q(b,prime(n))}$ が素数になるような最小の底 b は

2, 2, 2, 2, 2, 2, 2, 2, 7, 2, 16, 61, 2, 6, 10, 6, 2, 5, 46, 18, 2, 49, 16, 70, 2, 5, 6, 12, 92, 2, 48, 89, 30, 16, 147, 19, 19, 2, 16, 11, 289, 2, 12, 52, 2, 66, 9, 22, 5, 489, 69, 137, 16, 36, 96, 76, 117, 26, 3, ... (この列は n = 2 で始まる) オンライン整数列大辞典の数列 A103795

脚注

外部リンク

• John Renze and Eric W. Weisstein. "Wagstaff prime". mathworld.wolfram.com (英語).
• Chris Caldwell, The Top Twenty: Wagstaff at The Prime Pages.
• Renaud Lifchitz, "An efficient probable prime test for numbers of the form (2^p   1)/3".
• Tony Reix, "Three conjectures about primality testing for Mersenne, Wagstaff and Fermat numbers based on cycles of the Digraph under x² − 2 modulo a prime".
• repunit in base -50 to 50